Análisis de brotes en tiempo real: el ébola como estudio de caso - parte 2

11 June 2019 / [practicals] / #simulation #response #ebola #epicurve #reproduction number #Spanish

Introducción

Esta práctica es la segunda parte (de tres) de una práctica que simula la evaluación temprana y la reconstrucción de un brote de enfermedad por el virus del Ébola (EVE). Asegúrese de haber pasado por la parte 1 antes de comenzar la parte 2. En la parte 2 de la práctica, presentamos varios aspectos del análisis de la etapa inicial de un brote, incluida la estimación de la tasa de crecimiento, los datos del rastreo de contactos, los atrasos y las estimaciones de transmisibilidad. La parte 3 de la práctica ofrecerá una introducción a la reconstrucción de la cadena de transmisión mediante el uso de outbreaker2.

Nota: Esta práctica se deriva de las prácticas Ebola simulation part 1: early outbreak assessment y Ebola simulation part 2: outbreak reconstruction

Resultados del aprendizaje

Al final de esta práctica (parte 2), será capaz de:

Estimar e interpretar la tasa de crecimiento y el tiempo en que se duplica la epidemia.
Estimar el intervalo de serie a partir de los datos pareados de individuos infectantes/ individuos infectados.
Estimar e interpretar el número de reproducción de la epidemia.
Prever a corto plazo la incidencia futura

Contexto: un nuevo brote de EVE en un país ficticio de África occidental

Se ha notificado un nuevo brote de EVE en un país ficticio de África occidental. El Ministerio de Salud se encarga de coordinar la respuesta al brote, y lo ha contratado como consultor en análisis epidémico para informar la respuesta en tiempo real. Usted ya leyó un análisis descriptivo realizado de los datos (la parte 1 de la práctica). ¡Ahora hagamos algunos análisis estadísticos!

Paquetes necesarios

Los siguientes paquetes, disponibles en CRAN o github, son necesarios para este análisis. Estos programas los instalamos en la parte 1, pero si no es así, instale los paquetes necesarios de la siguiente manera:

# install.packages("remotes")
# install.packages("readxl")
# install.packages("outbreaks")
# install.packages("incidence")
# remotes::install_github("reconhub/epicontacts@ttree")
# install.packages("distcrete")
# install.packages("epitrix")
# remotes::install_github("annecori/EpiEstim")
# remotes::install_github("reconhub/projections")
# install.packages("ggplot2")
# install.packages("magrittr")
# install.packages("binom")
# install.packages("ape")
# install.packages("outbreaker2")
# install.packages("here")

Una vez instalados los paquetes, es posible que deba abrir una nueva sesión de R. Luego cargue las bibliotecas de la siguiente manera:

library(readxl)
library(outbreaks)
library(incidence)
library(epicontacts)
library(distcrete)
library(epitrix)
library(EpiEstim)
library(projections)
library(ggplot2)
library(magrittr)
library(binom)
library(ape)
library(outbreaker2)
library(here)

Leer los datos procesados en la parte 1

i_daily <- readRDS("data/clean/i_daily.rds")
i_weekly <- readRDS("data/clean/i_weekly.rds")
linelist <- readRDS("data/clean/linelist.rds")
linelist_clean <- readRDS("data/clean/linelist_clean.rds")
contacts <- readRDS("data/clean/contacts.rds")

Estimación de la tasa de crecimiento mediante un modelo log-lineal

El modelo de incidencia más simple es probablemente el modelo log-lineal, es decir, un modelo de regresión lineal sobre incidencias transformadas logarítmicamente. Para ello trabajaremos con incidencia semanal, para evitar tener demasiados problemas con incidencia cero (que no se pueden registrar).

Grafique la incidencia transformada logarítmicamente:

ggplot(as.data.frame(i_weekly)) + 
  geom_point(aes(x = dates, y = log(counts))) + 
  scale_x_incidence(i_weekly) +
  xlab("date") +
  ylab("log weekly incidence") + 
  theme_minimal()

¿Qué le dice esta gráfica sobre la epidemia?

En el paquete incidence , la funciónfit estimará los parámetros de este modelo a partir de un objeto de incidencia (aquí, i_weekly ). Aplíquelo a los datos y almacene el resultado en un nuevo objeto llamado f . Puede imprimir y usar f para derivar estimaciones de la tasa de crecimiento r y el tiempo de duplicación, y agregar el modelo correspondiente a la gráfica de incidencia:

Ajuste un modelo log-lineal a los datos de incidencia semanal:

f <- incidence::fit(i_weekly)

## Warning in incidence::fit(i_weekly): 1 dates with incidence of 0 ignored for
## fitting

## <incidence_fit object>
## 
## $model: regression of log-incidence over time
## 
## $info: list containing the following items:
##   $r (daily growth rate):
## [1] 0.04145251
## 
##   $r.conf (confidence interval):
##           2.5 %     97.5 %
## [1,] 0.02582225 0.05708276
## 
##   $doubling (doubling time in days):
## [1] 16.72148
## 
##   $doubling.conf (confidence interval):
##         2.5 %   97.5 %
## [1,] 12.14285 26.84302
## 
##   $pred: data.frame of incidence predictions (12 rows, 5 columns)

plot(i_weekly, fit = f)

Mirando la gráfica y el ajuste, ¿cree que este es un ajuste razonable?

Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los retrasos observados

Utilizando la gráfica del logaritmo (incidencia) que grafico anteriormente, y pensando en por qué el crecimiento exponencial no puede observarse en las últimas semanas, elija una fecha límite y ajuste el modelo logarítmico lineal a una sección adecuada de la epicurva donde crea que puede estimar de manera más confiable la tasa de crecimiento r, y el tiempo de duplicación.

Es posible que desee examinar cuánto tiempo después de la aparición de los síntomas los casos son hospitalizados; para obtener un reporte de una fecha especifica, siga estos comandos:

summary(as.numeric(linelist_clean$date_of_hospitalisation - linelist_clean$date_of_onset))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00    1.00    2.00    3.53    5.00   22.00

suponiendo que los casos solo se notifiquen durante la hospitalización o después de ella, vemos que la hospitalización toma en promedio 4 días, pero hay retrasos de hasta 22 días, por lo que las demoras en la notificación pueden ser largas y es sensato asumir que es probable que los datos de las últimas dos o tres semanas estén incompletos.
El crecimiento exponencial se observa solo hasta principios o principios o mediados de junio
Es probable que esto se deba a la demora entre el inicio y la notificación. Esto significa que los casos de inicio más reciente no se han informado y no aparecen en la base de datos de casos
Cuando solo se mira la epicurva puede resultar en una interpretación potencialmente errónea de las tendencias recientes en la incidencia.

# cuántas semanas debe descartar al final de la epicurva 
n_weeks_to_discard <-

# cuántas semanas debe descartar al final de la epicurva
n_weeks_to_discard <- 2

min_date <- min(i_daily$dates)
max_date <- max(i_daily$dates) - n_weeks_to_discard * 7
# Para truncar la incidencia semanal 
i_weekly_trunc <- subset(i_weekly, 
                         from = min_date, 
                         to = max_date) # descarte las últimas semanas de datos
# incidencia diaria truncada 
# no la usamos para la regresión lineal pero se puede usar más adelante
i_daily_trunc <- subset(i_daily, 
                         from = min_date, 
                         to = max_date) # eliminamos las últimas dos semanas de datos

Vuelva a montar y a graficar el modelo logarítmico lineal, pero utilizando los datos truncados i_weekly_trunc.

f <- incidence::fit(i_weekly_trunc)
f

## <incidence_fit object>
## 
## $model: regression of log-incidence over time
## 
## $info: list containing the following items:
##   $r (daily growth rate):
## [1] 0.04773599
## 
##   $r.conf (confidence interval):
##           2.5 %     97.5 %
## [1,] 0.03141233 0.06405965
## 
##   $doubling (doubling time in days):
## [1] 14.52043
## 
##   $doubling.conf (confidence interval):
##         2.5 %   97.5 %
## [1,] 10.82034 22.06609
## 
##   $pred: data.frame of incidence predictions (11 rows, 5 columns)

plot(i_weekly_trunc, fit = f)

Observe las estadísticas resumidas de su ajuste:

summary(f$model)

## 
## Call:
## stats::lm(formula = log(counts) ~ dates.x, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.79781 -0.44508 -0.00138  0.35848  0.69880 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.296579   0.320461   0.925    0.379    
## dates.x     0.047736   0.007216   6.615 9.75e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5298 on 9 degrees of freedom
## Multiple R-squared:  0.8294, Adjusted R-squared:  0.8105 
## F-statistic: 43.76 on 1 and 9 DF,  p-value: 9.754e-05

Puede observar la bondad del ajuste (Rsquared), la pendiente estimada (tasa de crecimiento/growth rate) y el tiempo de duplicación correspondiente como se muestra a continuación:

# ¿El modelo se ajusta bien a los datos?
adjRsq_model_fit <- summary(f$model)$adj.r.squared
# ¿ Cuál es la tasa de crecimiento estimada de la epidemia?
daily_growth_rate <- f$model$coefficients['dates.x']
# intervalo de confianza:
daily_growth_rate_CI <- confint(f$model, 'dates.x', level=0.95)
# ¿Cuál es el tiempo de duplicación de la epidemia?
doubling_time_days <- log(2) / daily_growth_rate
# intervalo de confianza:
doubling_time_days_CI <- log(2) / rev(daily_growth_rate_CI)

Aunque el log-lineal es un método simple y rápido para la evaluación temprana de una epidemia, se debe tener cuidado de ajustar solo hasta el punto en que haya un crecimiento epidémico. Tenga en cuenta que puede resultar difícil definir este punto.

El modelo log-lineal no se puede aplicar fácilmente si hay días sin casos, ya que no puede tomar el registro de 0). Aquí hemos agregado los datos semanales para evitar este problema y hemos establecido semanas con 0 casos como NA, por lo que se ignoran en el análisis. N - Aquí tuvimos bastantes semanas de datos con los que trabajar, pero al principio de un brote, un análisis similar puede llevar a estimaciones muy inciertas de la tasa de crecimiento y el tiempo de duplicación debido al tamaño pequeño de la muestra. n - Si los datos sobre las demoras en los informes hubieran estado disponibles, se podría haber tomado una decisión más informada sobre el número de semanas / días para descartar.

Seguimiento de contactos: vigile los contactos

El rastreo de contactos es uno de los pilares de la respuesta a un brote de ébola. Esto implica identificar y hacer un seguimiento de las personas en riesgo que hayan tenido contacto con un caso conocido, es decir, que puedan haber sido infectadas. Para el ébola, los contactos se vigilan durante 21 días (el límite superior del período de incubación). Esto asegura que los contactos que se vuelven sintomáticos puedan aislarse rápidamente, reduciendo la posibilidad de una mayor transmisión. Para esto usamos la base de datos de casos completa en lugar de linelist_clean donde descartamos las entradas con errores en las fechas, porque apesar del error el contacto aún puede ser válido.

Usando la función make_epicontacts en el paquete epicontacts paquete, cree un nuevo objeto epicontacts llamado epi_contacts . Asegúrese de comprobar los nombres de las columnas de los argumentos relevantes “ to ” y “from” .

epi_contacts <- make_epicontacts(linelist = linelist, contacts = contacts, 
                                 id = "case_id", # nombre del identificador en la base de datos de casos
                                 from = "infector", # nombre de la columna 'from' en los contactos
                                 to = "case_id",  # nombre de la columna 'to' en los contactos
                                 directed = TRUE)

epi_contacts

## 
## /// Epidemiological Contacts //
## 
##   // class: epicontacts
##   // 169 cases in linelist; 60 contacts;  directed 
## 
##   // linelist

## Warning: `tbl_df()` was deprecated in dplyr 1.0.0.
## Please use `tibble::as_tibble()` instead.

## # A tibble: 169 x 11
##    id     generation date_of_infection date_of_onset date_of_hospitalisation
##    <chr>       <dbl> <date>            <date>        <date>                 
##  1 d1fafd          0 NA                2014-04-07    2014-04-17             
##  2 53371b          1 2014-04-09        2014-04-15    2014-04-20             
##  3 f5c3d8          1 2014-04-18        2014-04-21    2014-04-25             
##  4 6c286a          2 NA                2014-04-27    2014-04-27             
##  5 0f58c4          2 2014-04-22        2014-04-26    2014-04-29             
##  6 49731d          0 2014-03-19        2014-04-25    2014-05-02             
##  7 f9149b          3 NA                2014-05-03    2014-05-04             
##  8 881bd4          3 2014-04-26        2014-05-01    2014-05-05             
##  9 e66fa4          2 NA                2014-04-21    2014-05-06             
## 10 20b688          3 NA                2014-05-05    2014-05-06             
## # ... with 159 more rows, and 6 more variables: date_of_outcome <date>,
## #   outcome <chr>, gender <chr>, hospital <chr>, lon <dbl>, lat <dbl>
## 
##   // contacts
## 
## # A tibble: 60 x 3
##    from   to     source 
##    <chr>  <chr>  <chr>  
##  1 d1fafd 53371b other  
##  2 f5c3d8 0f58c4 other  
##  3 0f58c4 881bd4 other  
##  4 f5c3d8 d58402 other  
##  5 20b688 d8a13d funeral
##  6 2ae019 a3c8b8 other  
##  7 20b688 974bc1 funeral
##  8 2ae019 72b905 funeral
##  9 40ae5f b8f2fd funeral
## 10 f1f60f 09e386 other  
## # ... with 50 more rows

Usted puede graficar fácilmente estos contactos, pero con un poco de ajuste (ver ?vis_epicontacts) puede personalizar, por ejemplo, símbolos por género y colores de flechas por fuente de exposición (u otras variables de interés):

# por ejemplo, observe la fuente de infección reportada de los contactos.
table(epi_contacts$contacts$source, useNA = "ifany")

## 
## funeral   other 
##      20      40

p <- plot(epi_contacts, node_shape = "gender", shapes = c(m = "male", f = "female"), node_color = "gender", edge_color = "source", selector = FALSE)
p

Usando la función match ( ver? Match ) verifique que los contactos visualizados sean realmente casos.

match(contacts$case_id, linelist$case_id)

##  [1]   2   5   8  14  15  16  18  20  21  22  24  25  26  27  30  33  37  38  40
## [20]  46  48  51  58  59  62  64  68  69  70  71  73  75  79  84  86  88  90  94
## [39]  95  96  98 103 108 115 116 122 126 131 133 142 145 146 147 148 153 155 157
## [58] 160 162 166

Una vez se asegure de que todos estos son casos, mire la red:

¿Parece que hay superpropagación (transmisión heterogénea)?
Al observar el género de los casos, ¿puede deducir algo de esto? ¿Existen diferencias visibles por género?
Parece haber una superpropagación, y algunos casos provienen de un solo caso (11f8ea infecta a otros 5 individuos. No parece haber diferencias inmediatas entre el género de los casos

Estimación de la transmisibilidad ( $R$ )

Modelo de proceso de ramificación

La transmisibilidad de la enfermedad puede evaluarse mediante la estimación del número de reproducción R, definido como el número esperado de casos secundarios por caso infectado. En las primeras etapas de un brote, y asumiendo una gran población sin inmunidad, esta cantidad es también el número de reproducción básico $R_0$ , es decir, $R$ en una gran población totalmente susceptible.

El paquete EpiEstim implementa una estimación bayesiana de $R$ , utilizando las fechas de inicio de los síntomas y la información sobre la distribución del intervalo de serie, es decir, la distribución del tiempo desde el inicio de los síntomas en un caso y el inicio de los síntomas en quien lo infecto (infectante) (ver Cori et al., 2013, AJE 178: 1505-1512).

En resumen, EpiEstim usa un modelo simple que describe la incidencia en un día dado como la distribución de Poisson, con una media determinada por la fuerza total de infección en ese día:

$$ I_t ∼ Poisson(\lambda_t)$$

donde $I_t$ es la incidencia (basada en la aparición de los síntomas), $t$ es el día y $\lambda_t$ es la fuerza de la infección ese día. Teniendo en cuenta R el número de reproducción y w () la distribución de intervalo de serie discreta, tenemos:

$$\lambda_t = R \sum_{s=1}^t I_sw(t-s)$$

La verosimilitud (probabilidad de observar los datos dados el modelo y los parámetros) se define como una función de R:

$$L(I) = p(I|R) = \prod_{t = 1}^{T} f_P(I_t, \lambda_t)$$

donde $f_P(.,\mu)$ es la función de masa de probabilidad de una distribución de Poisson con media $\mu$ .

Estimación del intervalo de serie (SI)

Dado que los datos se recopilaron sobre pares de individuos infectantes e infectados, esto debería ser suficiente para estimar la distribución del intervalo en serie. Si ese no fuera el caso, podríamos haber utilizado datos de brotes pasados en su lugar.

Utilice la función get_pairwise para extraer el intervalo de la serie, es decir, la diferencia en la fecha de aparición entre los individuos infectantes e infectados:

si_obs <- get_pairwise(epi_contacts, "date_of_onset")
summary(si_obs)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   5.000   6.500   9.117  12.250  30.000

## Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## 1.000   5.000   6.500   9.117  12.250  30.000 
hist(si_obs, breaks = 0:30,
     xlab = "Días después de la aparición de los síntomas", ylab = "Frecuencia",
     main = "Intervalo de serie (distribución empírica)",
     col = "grey", border = "white")

¿Qué opina de esta distribución? Realice cualquier ajuste que considere necesario y luego use la función fit_disc_gamma del paqueteepitrix para ajustar estos datos a una distribución Gamma de valores discretos. Sus resultados deberían verse aproximadamente como:

si_fit <- fit_disc_gamma(si_obs, w = 1)
si_fit

## $mu
## [1] 8.612892
## 
## $cv
## [1] 0.7277355
## 
## $sd
## [1] 6.267907
## 
## $ll
## [1] -183.4215
## 
## $converged
## [1] TRUE
## 
## $distribution
## A discrete distribution
##   name: gamma
##   parameters:
##     shape: 1.88822148063956
##     scale: 4.5613778865727

si_fit contiene información diversa sobre los retrasos ajustados, incluida la distribución estimada en la ranura $distribution. Puede comparar esta distribución con los datos empíricos en la siguiente gráfica:

si <- si_fit$distribution
si

## A discrete distribution
##   name: gamma
##   parameters:
##     shape: 1.88822148063956
##     scale: 4.5613778865727

## compare fitted distribution
hist(si_obs, xlab = "Días después de la aparición de los síntomas", ylab = "Frecuencia",
     main = "Intervalo de serie: ajustar a los datos", col = "salmon", border = "white",
     50, ylim = c(0, 0.15), freq = FALSE, breaks = 0:35)
points(0:60, si$d(0:60), col = "#9933ff", pch = 20)
points(0:60, si$d(0:60), col = "#9933ff", type = "l", lty = 2)

¿Confiaría en esta estimación del tiempo de generación? ¿Cómo lo compararía con las estimaciones reales del brote de EVE en África occidental (Equipo de respuesta al ébola de la OMS (2014) NEJM 371: 1481–1495) con una media de 15,3 días y una desviación estándar de 9,3 días?

distribución sesgada con una media mucho más corta que la estimada en NEJM 371:1481–1495
la gran mayoría de las parejas tienen un SI <15 días
los casos pueden recordar con mayor precisión sus exposiciones recientes, lo que puede llevar a una subestimación del intervalo de serie
al estimar el intervalo de serie en tiempo real, es posible que aún no se hayan observado intervalos de serie más largos debido a la censura por la derecha
esta estimación se basa en pocas observaciones, por lo que hay incertidumbre en las estimaciones del intervalo de serie

Estimación del número de reproducción

Ahora que tenemos estimaciones del intervalo de la serie, podemos usar esta información para estimar la transmisibilidad de la enfermedad (medida por $R_0$ ). Asegúrese de utilizar el objeto de incidencia diaria (no semanal) truncado al período en el que ha decidido que hay un crecimiento exponencial (i_daily_trunc).

Utilizando las estimaciones de la media y la desviación estándar del intervalo de serie que acaba de obtener, utilice la función estimate_R para estimar el número de reproducción (consulte ?estimate_R) y almacene el resultado en un nuevo objeto R .

Antes de usar estimate_R, necesita crear un objetoconfig usando la función make_config , donde usted debe especificar la ventana de tiempo en la cual desea estimar el número de reproducción, así como elmean_si y std_si a usar . Para la ventana de tiempo, use t_start = 2 (solo puede estimar R apartir del día 2 en adelante, dado que está condicionando la incidencia observada en el pasado) y especifique t_end = length(i_daily_trunc$counts)para estimar R hasta la último fecha de su incidencia truncadai_daily_trunc` .

config <- make_config(mean_si = si_fit$mu, # media de la distribución si estimada anteriormente
                      std_si = si_fit$sd,  # desviación estándar de la distribución si estimada anteriormente
                      t_start = 2,         # día de inicio de la ventana de tiempo
                      t_end = length(i_daily_trunc$counts)) # último día de la ventana de tiempo

R <- # use estimate_R usando el método = "parametric_si"
plot(R, legend = FALSE)

R <- estimate_R(i_daily_trunc, method = "parametric_si", config = config)
plot(R, legend = FALSE)

Extraiga la mediana y los intervalos de credibilidad del 95% (95% CrI) para el número de reproducción de la siguiente manera:

R_median <- R$R$`Median(R)`
R_CrI <- c(R$R$`Quantile.0.025(R)`, R$R$`Quantile.0.975(R)`)
R_median

## [1] 1.278192

R_CrI

## [1] 1.068374 1.513839

Interprete estos resultados: ¿qué opina del número de reproducción? ¿Qué refleja? Con base en la última parte de la epicurva, algunos colegas sugieren que la incidencia está disminuyendo y que el brote puede estar bajo control. ¿Qué opina de esto?

Tenga en cuenta que estos resultados dependen en gran medida del intervalo de serie estimado; un SI medio más alto conducirá a estimaciones de R más altas.
Los resultados también serán sensibles al número de puntos de datos descartados hacia el final de los datos disponibles.

Tenga en cuenta que podría haber estimado R0 directamente a partir de la tasa de crecimiento y el intervalo de serie, utilizando la fórmula descrita en Wallinga y Lipsitch, Proc Biol Sci, 2007:

$R_0 = \frac{1}{\int_{s=0}^{+\infty}e^{-rs}w(s)ds}$ , e implementando la función r2R0 del paquete epitrix. Aunque esto puede parecer una fórmula complicada, el razonamiento detrás de ella es simple y se ilustra en la figura siguiente: para una curva de incidencia observada que crece exponencialmente, si conoce el intervalo de serie, puede derivar el número de reproducción.

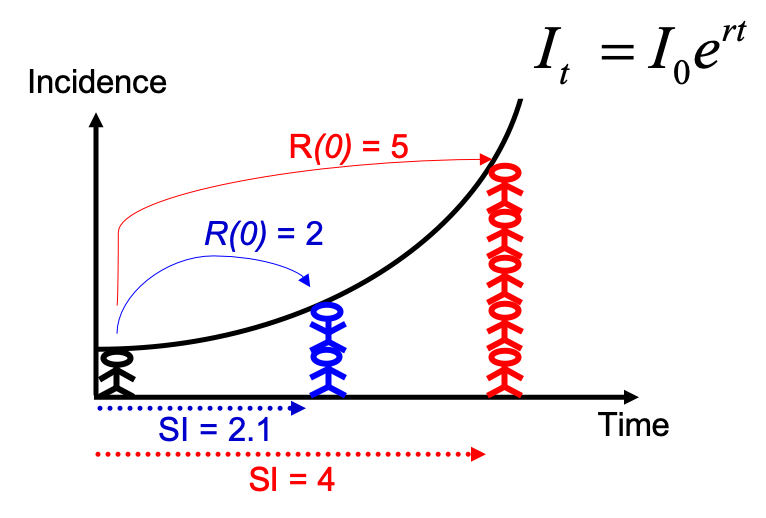
Estimación de R0 a partir de la tasa de crecimiento y el intervalo de
serie.

En comparación con la figura anterior, hay incertidumbre en la tasa de crecimiento r, y el intervalo de serie tiene una distribución completa en lugar de un valor único. Esto se puede tener en cuenta al estimar R de la siguiente manera:

# genere una muestra de estimaciones de R0 a partir de la tasa de crecimiento y el intervalo de serie que estimamos anteriormente 
R_sample_from_growth_rate <- lm2R0_sample(f$model, # modelo log-lineal que contiene nuestras estimaciones de la tasa de crecimiento r
                                          si$d(1:100), # distribución de intervalo de serie (truncado después de 100 días)
                                          n = 1000) # tamaño de muestra deseado
# Grafique esto:
hist(R_sample_from_growth_rate)

# ¿Cuál es la mediana?
R_median_from_growth_rate <- median(R_sample_from_growth_rate)
R_median_from_growth_rate # compare with R_median

## [1] 1.418092

# ¿ Cuál es el IC del 95%?
R_CI_from_growth_rate <- quantile(R_sample_from_growth_rate, c(0.025, 0.975))
R_CI_from_growth_rate # compare con R_CrI

##     2.5%    97.5% 
## 1.266280 1.581886

Tenga en cuenta que las estimaciones anteriores son ligeramente diferentes de las obtenidas utilizando el modelo de proceso de ramificación. Hay algunas razones para esto. En primer lugar, usted utilizó datos más detallados (incidencia diaria frente a incidencia semanal) para la estimación del proceso de ramificación (EpiEstim). Además, el modelo log-lineal pone el mismo peso en todos los puntos de datos, mientras que el modelo de proceso de ramificación pone un peso diferente en cada punto de datos (dependiendo de la incidencia observada en cada paso de tiempo). Esto puede llevar a estimaciones de R ligeramente diferentes.

Previsión de incidencia a corto plazo

La función project del paquete projections se puede utilizar para simular trayectorias epidémicas plausibles simulando la incidencia diaria utilizando el mismo proceso de ramificación que se utilizó para estimar $R$ en EpiEstim. Todo lo que se necesita es uno o varios valores de $R$ y una distribución de intervalo en serie, almacenados como un objeto distcrete.

Aquí, primero ilustramos cómo podemos simular 5 trayectorias aleatorias usando un valor fijo de $R$ = 1.28, la estimación mediana de R desde arriba.
Utilice el mismo objeto de incidencia truncado diario que el anterior para simular una incidencia futura.

#?project
small_proj <- project(i_daily_trunc,# objeto de incidencia
                      R = R_median, # R estimado a utilizar
                      si = si,      # distribución de intervalo de serie
                      n_sim = 5,    # simula 5 trayectorias
                      n_days = 10,  # durante 10 días
                      R_fix_within = TRUE) # mantiene el mismo valor de R todos los días

# mire cada trayectoria proyectada (como columnas):
as.matrix(small_proj)

##            [,1] [,2] [,3] [,4] [,5]
## 2014-06-18    5    3    8    4    4
## 2014-06-19    2    4    6    4    0
## 2014-06-20    6    3    5    5    2
## 2014-06-21    3    1    6    2    6
## 2014-06-22    5    6    7    7    1
## 2014-06-23    4    2   10    3    6
## 2014-06-24    4    8    6    7    1
## 2014-06-25    6    5   13    3    3
## 2014-06-26    3    5    4    2    2
## 2014-06-27    2    3    8    1    2
## attr(,"class")
## [1] "matrix" "array"

Puede usar un solo valor R para toda la trayectoria (R_fix_within = TRUE) o volver a muestrear R en cada paso de tiempo (R_fix_within = FALSE).
R_fix_within = TRUE significa que la trayectoria está asociada con un solo valor R y es más fácil de entender
Esto también da valores más extremos de R y proyecciones más conservadoras

Usando el mismo principio, genere 1,000 trayectorias durante las próximas 2 semanas, usando un rango de valores plausibles de $R$ .
La distribución posterior de R tiene una distribución gamma (ver Cori et al. AJE 2013), por lo que puede usar la función rgamma para extraer valores aleatoriamente de esa distribución. También necesitará utilizar la función gamma_mucv2shapescale del paquete epitrix como se muestra a continuación.

sample_R <- function(R, n_sim = 1000)
{
  mu <- R$R$`Mean(R)`
  sigma <- R$R$`Std(R)`
  Rshapescale <- gamma_mucv2shapescale(mu = mu, cv = sigma / mu)
  R_sample <- rgamma(n_sim, shape = Rshapescale$shape, scale = Rshapescale$scale)
  return(R_sample)
}
R_sample <- sample_R(R, 1000) # obtiene una muestra de 1000 valores de R de la distribución posterior
hist(R_sample, col = "grey")  # Grafíca un histograma de la muestra 
abline(v = R_median, col = "red") # muestra la mediana estimada de R como una línea vertical roja sólida
abline(v = R_CrI, col = "red", lty = 2) # muestra el 95% de CrI de R como líneas verticales punteadas rojas

Almacene los resultados de sus nuevas proyecciones en un objeto llamado proj.

proj <- project(x = i_daily_trunc, 
                R = R_sample, # ahora usando una muestra de valores R
                si = si, 
                n_sim = 1000, 
                n_days = 14, # proyecto durante 2 semanas
                R_fix_within = TRUE)

Puede visualizar las proyecciones de la siguiente manera:

plot(i_daily_trunc) %>% add_projections(proj, c(0.025, 0.5, 0.975))

## Scale for 'x' is already present. Adding another scale for 'x', which will
## replace the existing scale.

¿Cómo interpretaría el siguiente resumen de las proyecciones?

apply(proj, 1, summary)

##         2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23
## Min.          0.00      0.000      0.000      0.000       0.00      0.000
## 1st Qu.       2.00      2.000      3.000      3.000       3.00      3.000
## Median        4.00      4.000      4.000      4.000       4.00      4.000
## Mean          3.86      3.981      4.154      4.407       4.46      4.701
## 3rd Qu.       5.00      5.000      5.000      6.000       6.00      6.000
## Max.         13.00     11.000     12.000     12.000      13.00     13.000
##         2014-06-24 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29
## Min.         0.000      0.000      0.000      0.000      0.000      0.000
## 1st Qu.      3.000      3.000      3.000      3.000      3.000      4.000
## Median       5.000      5.000      5.000      5.000      5.000      5.000
## Mean         4.707      4.751      4.989      5.096      5.253      5.506
## 3rd Qu.      6.000      6.000      7.000      7.000      7.000      7.000
## Max.        17.000     15.000     16.000     15.000     18.000     19.000
##         2014-06-30 2014-07-01
## Min.         0.000      0.000
## 1st Qu.      4.000      4.000
## Median       5.000      6.000
## Mean         5.762      5.754
## 3rd Qu.      8.000      8.000
## Max.        18.000     17.000

apply(proj, 1, function(x) mean(x > 0)) # proporción de trayectorias con al menos

## 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##      0.982      0.985      0.984      0.986      0.987      0.989      0.986 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 2014-07-01 
##      0.983      0.987      0.991      0.986      0.992      0.993      0.992

                                        # un caso en cada día contemplado
apply(proj, 1, mean) # número medio diario de casos

## 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##      3.860      3.981      4.154      4.407      4.460      4.701      4.707 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 2014-07-01 
##      4.751      4.989      5.096      5.253      5.506      5.762      5.754

apply(apply(proj, 2, cumsum), 1, summary) # muestra la proyección del número acumulado de casos en

##         2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23
## Min.          0.00      0.000      3.000      5.000      8.000     10.000
## 1st Qu.       2.00      6.000     10.000     13.000     17.000     21.000
## Median        4.00      8.000     12.000     16.000     21.000     25.000
## Mean          3.86      7.841     11.995     16.402     20.862     25.563
## 3rd Qu.       5.00     10.000     14.000     19.000     24.000     30.000
## Max.         13.00     18.000     25.000     33.000     44.000     54.000
##         2014-06-24 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29
## Min.         12.00     12.000      15.00     16.000     19.000     20.000
## 1st Qu.      25.00     29.000      32.00     37.000     41.000     46.000
## Median       30.00     34.000      39.00     44.000     49.000     55.000
## Mean         30.27     35.021      40.01     45.106     50.359     55.865
## 3rd Qu.      35.00     41.000      47.00     53.000     58.000     65.000
## Max.         61.00     73.000      89.00    102.000    120.000    139.000
##         2014-06-30 2014-07-01
## Min.        25.000     25.000
## 1st Qu.     50.000     55.000
## Median      60.000     66.000
## Mean        61.627     67.381
## 3rd Qu.     72.000     79.000
## Max.       155.000    168.000

                                          # las próximas dos semanas

apply(proj, 1, summary) muestra un resumen de la incidencia en cada día
apply(proj, 1, function(x) mean(x > 0)) muestra la proporción de trayectorias con al menos un caso en cada día contemplado
apply(proj, 1, mean) muestra el número medio diario de casos
apply(apply(proj, 2, cumsum), 1, summary) muestra la proyección del número adicional de casos acumulados en las próximas dos semanas

Según estos resultados, ¿cuáles son las posibilidades de que aparezcan más casos en un futuro próximo? ¿Se está controlando este brote? ¿Recomendaría ampliar o reducir la respuesta? ¿Es esto consistente con su estimación de $R$ ?

la incertidumbre es amplia y se hace más amplia cuanto más avance en el futuro.
la tendencia central sugiere un número creciente de casos
esto se basa en la suposición de que la transmisibilidad se ha mantenido constante durante el transcurso del brote hasta ahora y permanecerá constante en el futuro
todo esto se basa en nuestra distribución estimada de intervalo de serie - un SI medio más alto conduciría a estimaciones de R más grandes y, por lo tanto, a proyecciones de incidencia más pesimistas.

¡Pare!

Por favor, informe a un tutor cuando haya llegado a este punto antes de continuar.

Tenga en cuenta la incertidumbre en las estimaciones del intervalo de serie al estimar el número de reproducción

Tenga en cuenta que esta sección es independiente de las siguientes, omita si no tiene tiempo.

EpiEstim permite tener en cuenta explícitamente la incertidumbre en las estimaciones del intervalo de serie debido al tamaño limitado de la muestra de pares de individuo infetante / individuo infectado. Tenga en cuenta que también permite tener en cuenta la incertidumbre sobre las fechas de inicio de los síntomas para cada uno de estos pares (que no es necesario aquí).

Utilice la opción method = "si_from_data" en estimate_R. Para utilizar esta opción, debe crear un marco de datos con 4 columnas: EL, ER, SL y SR. (L) para el límite izquierdo y ® para el límite derecho del tiempo observado de síntomas para los casos infectantes (E) e infectados (S). Aquí derivamos esto de si_obs de la siguiente manera:

si_data <- data.frame(EL = rep(0L, length(si_obs)), 
                      ER = rep(1L, length(si_obs)), 
                      SL = si_obs, SR = si_obs + 1L)

A continuación, podemos introducir esto en estimate_R (pero esto llevará algún tiempo para ejecutarse, ya que estima la distribución del intervalo de serie utilizando un MCMC y tiene en cuenta por completo la incertidumbre en el intervalo de serie para estimar el número de reproducción).

config <- make_config(t_start = 2, 
                      t_end = length(i_daily_trunc$counts))
R_variableSI <- estimate_R(i_daily_trunc, method = "si_from_data", 
                           si_data = si_data,
                           config = config)

## Running 8000 MCMC iterations 
## MCMCmetrop1R iteration 1 of 8000 
## function value = -187.90259
## theta = 
##    0.52779
##    1.77629
## Metropolis acceptance rate = 1.00000
## 
## MCMCmetrop1R iteration 1001 of 8000 
## function value = -188.13150
## theta = 
##    1.06602
##    1.22659
## Metropolis acceptance rate = 0.54046
## 
## MCMCmetrop1R iteration 2001 of 8000 
## function value = -187.61607
## theta = 
##    1.07521
##    1.15209
## Metropolis acceptance rate = 0.54923
## 
## MCMCmetrop1R iteration 3001 of 8000 
## function value = -187.61627
## theta = 
##    0.87103
##    1.47071
## Metropolis acceptance rate = 0.55382
## 
## MCMCmetrop1R iteration 4001 of 8000 
## function value = -186.53495
## theta = 
##    0.67428
##    1.49221
## Metropolis acceptance rate = 0.55361
## 
## MCMCmetrop1R iteration 5001 of 8000 
## function value = -186.52036
## theta = 
##    0.67142
##    1.55717
## Metropolis acceptance rate = 0.55709
## 
## MCMCmetrop1R iteration 6001 of 8000 
## function value = -186.58825
## theta = 
##    0.88190
##    1.26135
## Metropolis acceptance rate = 0.55941
## 
## MCMCmetrop1R iteration 7001 of 8000 
## function value = -189.89797
## theta = 
##    0.60889
##    1.36339
## Metropolis acceptance rate = 0.55963
## 
## 
## 
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
## The Metropolis acceptance rate was 0.55750
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
## 
## Gelman-Rubin MCMC convergence diagnostic was successful.
## 
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ 
## Estimating the reproduction number for these serial interval estimates...
##  @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

# compruebe que la MCMC convergió
R_variableSI$MCMC_converged

## [1] TRUE

# grafique el resultado:
plot(R_variableSI)

Observe la nueva mediana estimada de R y el 95% de CrI: ¿en qué se diferencian de sus estimaciones anteriores? ¿Crees que el tamaño del conjunto de datos de contactos ha tenido un impacto en tus resultados?

R_variableSI_median <- R_variableSI$R$`Median(R)`
R_variableSI_CrI <- c(R_variableSI$R$`Quantile.0.025(R)`, R_variableSI$R$`Quantile.0.975(R)`)
R_variableSI_median

## [1] 1.297997

R_variableSI_CrI

## [1] 1.080796 1.546635

Estimación de la transmisibilidad variable en el tiempo

Cuando la suposición de que ( $R$ ) es constante en el tiempo se vuelve insostenible, una alternativa es estimar la transmisibilidad variable en el tiempo utilizando el número de reproducción instantánea ( $R_t$ ). Este enfoque, introducido por Cori et al. (2013), también se implementa en el paquete EpiEstim. Estima ( $ R_t $ ) para ventanas de tiempo personalizadas (el valor predeterminado es una sucesión de ventanas de tiempo deslizantes), utilizando la misma probabilidad de Poisson descrita anteriormente. A continuación, estimamos la transmisibilidad para ventanas de tiempo deslizantes de 1 semana (el valor predeterminado de estimate_R):

config = make_config(list(mean_si = si_fit$mu, std_si = si_fit$sd))  
# t_start y t_end se configuran automáticamente para estimar R en ventanas deslizantes para 1 semana de forma predeterminada.

Rt <-         # use estimate_R usando método = "parametric_si"
  
# mire las estimaciones de Rt más recientes:
tail(Rt$R[, c("t_start", "t_end", "Median(R)", 
             "Quantile.0.025(R)", "Quantile.0.975(R)")])

Rt <- estimate_R(incid = i_daily_trunc,      # objeto de incidencia
                 method = "parametric_si",   # use intervalo de serie paramétrico
                 config = config)            # configuración especificada arriba

## Default config will estimate R on weekly sliding windows.
##     To change this change the t_start and t_end arguments.

# mire las estimaciones de Rt más recientes:
tail(Rt$R[, c("t_start", "t_end", "Median(R)", 
             "Quantile.0.025(R)", "Quantile.0.975(R)")])

##    t_start t_end Median(R) Quantile.0.025(R) Quantile.0.975(R)
## 60      61    67 1.2417304         0.8144152          1.797603
## 61      62    68 1.0045473         0.6318309          1.501326
## 62      63    69 0.8404935         0.5074962          1.294848
## 63      64    70 1.0276438         0.6538993          1.522464
## 64      65    71 1.0335607         0.6576643          1.531230
## 65      66    72 1.0337804         0.6578041          1.531556

Grafique la estimación de $R$ sobre le tiempo:

plot(Rt, legend = FALSE)

## Warning: Removed 1 row(s) containing missing values (geom_path).

¿Cómo interpretaría este resultado? ¿Cuál es la salvedad de esta representación?

¿Qué habría concluido si en lugar de usar i_daily_trunc como se indicó anteriormente, hubiera usado toda la curva de epidemias, es decir, i_daily ?

Rt_whole_incid <-            # use estimate_R usando method = "parametric_si",
 # la misma configuración que la anterior pero i_daily en lugar de i_daily_trunc
    
# mire las estimaciones de Rt más recientes:
tail(Rt_whole_incid$R[, c("t_start", "t_end", 
                         "Median(R)", "Quantile.0.025(R)", "Quantile.0.975(R)")])

Rt_whole_incid <- estimate_R(incid = i_daily, 
                             method = "parametric_si", 
                             config = config)

## Default config will estimate R on weekly sliding windows.
##     To change this change the t_start and t_end arguments.

## Warning in estimate_R_func(incid = incid, method = method, si_sample = si_sample, : You're estimating R too early in the epidemic to get the desired
##             posterior CV.

tail(Rt_whole_incid$R[, c("t_start", "t_end", 
                         "Median(R)", "Quantile.0.025(R)", "Quantile.0.975(R)")])

##    t_start t_end Median(R) Quantile.0.025(R) Quantile.0.975(R)
## 74      75    81 1.2330741         0.8412787         1.7310657
## 75      76    82 1.0008292         0.6564151         1.4488601
## 76      77    83 0.9432201         0.6128291         1.3753773
## 77      78    84 0.8202251         0.5158976         1.2258508
## 78      79    85 0.7452526         0.4566772         1.1356909
## 79      80    86 0.5146158         0.2811874         0.8515131

# lo anterior infiere incorrectamente que la transmisibilidad reciente es <1

lo anterior asume un R constante dentro de una ventana de tiempo deslizante

Guardar datos y salidas

Este es el final de la parte 2 de la práctica. Antes de continuar con la parte 3, deberá guardar los siguientes objetos:

saveRDS(linelist, "data/clean/linelist.rds")
saveRDS(linelist_clean, "data/clean/linelist_clean.rds")
saveRDS(epi_contacts, "data/clean/epi_contacts.rds")
saveRDS(si, "data/clean/si.rds")

Sobre este documento

Contribuciones

Anne Cori, Natsuko Imai, Finlay Campbell, Zhian N. Kamvar & Thibaut Jombart: Versión inicial
José M. Velasco-España: Traducción de Inglés a Español
Andree Valle-Campos: Ediciones menores

Contribuciones son bienvenidas vía pull requests.

Análisis de brotes en tiempo real: el ébola como estudio de caso - parte 2

Introducción

Resultados del aprendizaje

Contexto: un nuevo brote de EVE en un país ficticio de África occidental

Paquetes necesarios

Leer los datos procesados en la parte 1

Estimación de la tasa de crecimiento mediante un modelo log-lineal

Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los retrasos observados

Seguimiento de contactos: vigile los contactos

Estimación de la transmisibilidad ( $R$ )

Modelo de proceso de ramificación

Estimación del intervalo de serie (SI)

Estimación del número de reproducción

Previsión de incidencia a corto plazo

¡Pare!

Tenga en cuenta la incertidumbre en las estimaciones del intervalo de serie al estimar el número de reproducción

Estimación de la transmisibilidad variable en el tiempo

Guardar datos y salidas

Sobre este documento

Contribuciones

Análisis de brotes en tiempo real: el ébola como estudio de caso - parte 1

Real-time outbreak analysis: Ebola as a case study - part 1

Introducción

Resultados del aprendizaje

Contexto: un nuevo brote de EVE en un país ficticio de África occidental

Paquetes necesarios

Leer los datos procesados en la parte 1

Estimación de la tasa de crecimiento mediante un modelo log-lineal

Encuentre una fecha límite adecuada para el modelo log-lineal, en función de los retrasos observados

Seguimiento de contactos: vigile los contactos

Estimación de la transmisibilidad ($R$)

Modelo de proceso de ramificación

Estimación del intervalo de serie (SI)

Estimación del número de reproducción

Previsión de incidencia a corto plazo

¡Pare!

Tenga en cuenta la incertidumbre en las estimaciones del intervalo de serie al estimar el número de reproducción

Estimación de la transmisibilidad variable en el tiempo

Guardar datos y salidas

Sobre este documento

Contribuciones

Estimación de la transmisibilidad ( $R$ )