VBD: Construyendo un modelo simple para Zika

10 June 2019 / practicals / #zika #compartmental models #Spanish

El objetivo de esta práctica es presentar los conceptos básicos del modelado de Enfermedades Transmitidas por Vectores o VBD (por sus siglas en inglés Vector Borne Disease) mediante el uso del programa R, con énfasis en el funcionamiento de los métodos; utilizando como ejemplo un modelo básico de infección por arbovirus.

En esta práctica, se comenzará por comprender los componentes que contribuyen a $R_0$ y cómo las posibles intervenciones influyen en la transmisión. Más adelante, el participante debe construir un modelo de transmisión del Zika para observar los efectos de varios parámetros.

Conceptos básicos

Desarrollaremos estos conceptos:

Inmunidad de rebaño
Biología del mosquito
Historia natural de las infecciones en humanos
Tasa de contacto
Denso dependencia
Modelos estructurados por inmigración/muerte y por edad
Control de infecciones y morbilidad / eliminación de infecciones
Estrategias de control (en vectores y en humanos)

Paquetes requeridos

Ingrese en R los siguientes comandos:

# install.packages("deSolve", dep = TRUE)
# install.packages("ggplot2")
# install.packages("gridExtra", dep = TRUE)

(Para ejecutarlos presione control+enter en Windows y command+enter en Mac) Cuando la instalación haya terminado, cargue los paquetes ingresando en R los siguientes comandos:

library(deSolve)
library(ggplot2)
library(gridExtra)

(Para ejecutarlos presione control+enter en Windows y command+enter en Mac)

Modelo básico de Zika

Sh : Humanos suceptibles
Ih : Humanos infectados/infecciosos
Rh : Humanos recuperados de la infección (inmunizados por vida)
Sv : Vectores susceptibles
Ev : Vectores expuestos
Iv : Vectores infectados

Diagrama de flujo (parte I)

En esta sección, realice un diagrama para conectar los diferentes compartimentos del modelo

Los parámetros

Son necesarios varios parámetros para conectar los diferentes compartimentos del modelo.

Revise en el material suplementario del artículo http://science.sciencemag.org/content/early/2016/07/13/science.aag0219 y observe la tabla de parámetros de este modelo.

Busque los valores de los parámetros del modelo. Tenga en cuenta que todos los parámetros usados tienen la misma unidad de tiempo (días).

Lv       <-        # Esperanza de vida de los mosquitos (en días)
Lh       <-        # Esperanza de vida de los humanos (en días)
Iph      <-        # Periodo infeccioso en humanos (en días)
IP       <-        # Periodo infeccioso en vectores (en días)
EIP      <-        # Período de incubación extrínseco en mosquitos adultos (en días)
muv      <-        # Mortalidad en mosquitos
muh      <-        # Mortalidad en humanos
gamma    <-        # Tasa de recuperación en humanos
delta    <-        # Tasa de incubación extrínseca
betah    <-        # Probabilidad de transmisión del vector al hospedador
betav    <-        # Probabilidad de transmisión del hospedador al vector
Nh       <-        # Número de humanos (Población de Cali 2.4 millones)
m        <-        # Proporción vector a humano
Nv       <-        # Número de vectores
R0       <-        # Número reproductivo
b        <-        sqrt((R0 ^2 * muv*(muv+delta) * (muh+gamma)) /
                   (m * betah * betav * delta)) # Tasa de picadura

TIME     <-        # Número de años que se va a simular

Modelo (Ecuaciones)

Humanos

$$\ \frac{dSh}{dt} = \mu_h N_h - \frac {\beta_h b}{N_h} S_h I_v - \mu_h S_h $$
$$\ \frac{dIh}{dt} = \frac {\beta_h b}{N_h}S_h I_v - (\gamma_h + \mu_h) I_h $$
$$\ \frac{dRh}{dt} = \gamma_h I_h - \mu_h R_h$$

Vectores

$$\ \frac{dSv}{dt} = \mu_v N_v - \frac{\beta_v b} {N_h} I_h S_v - \mu_v Sv$$
$$\ \frac{dE_v}{dt} = \frac{\beta_v b} {N_h} I_h S_v - (\delta + \mu_v) Ev$$
$$\ \frac{dI_v}{dt} = \delta Ev - \mu_v I_v$$

Estimemos $R_0$ (Número reproductivo)

Formula necesaria para estimar $R_0$ :

$$ R_0^2 = \frac{mb^2 \beta_h \beta_v \delta}{\mu_v (\mu_v+\delta)(\mu_h+\gamma_h)} $$

Diagrama de flujo (parte II)

Ahora que conoce las ecuaciones, complete el diagrama de flujo con los parámetros y la conexión correcta entre los diferentes compartimentos.

Para finalizar, modele en R

Después de elaborar el diagrama de flujo y tener las ecuaciones, complete el modelo de abajo con los parámetros correctos (PAR)

arbovmodel <- function(t, x, params) {
  
  Sh <- x[1]    # Humanos suceptibles
  Ih <- x[2]    # Humans infectados 
  Rh <- x[3]    # Humanos recuperados
  Sv <- x[4]    # Vectores suceptibles
  Ev <- x[5]    # Vectores expuestos
  Iv <- x[6]    # Vectores infectados
  
  with(as.list(params), # entorno local para evaluar derivados
       {
         # Humanos
         dSh   <-  PAR * Nh - (PAR * PAR/Nh) * Sh * Iv - PAR * Sh   
         dIh   <-  (PAR * PAR/Nh) * Sh * Iv  - (PAR + PAR) * Ih
         dRh   <-  PAR * Ih  - PAR * Rh
         
         # Vectores
         dSv  <-  muv * Nv - (PAR* PAR/Nh) * Ih * Sv - PAR * Sv 
         dEv  <-  (PAR * PAR/Nh) * Ih * Sv - (PAR + PAR)* Ev
         dIv  <-  PAR * Ev - PAR * Iv
         
         dx   <- c(dSh, dIh, dRh, dSv, dEv, dIv)
         list(dx)
       }
  )
}

Resuelva el Sistema

En esta sección, complete and comente el código para:

Los VALORES para las condiciones iniciales del sistema
Los ARGUMENTOS de la función ode en el paquete deSolve.

# Tiempo 
times  <- seq(1, 365 * TIME , by = 1)

# Especifique los parametros
params <- c(
  muv      = muv,     
  muh      = muh,     
  gamma    = gamma,   
  delta    = delta,   
  b        = b,       
  betah    = betah,   
  betav    = betav,   
  Nh       = Nh,      
  Nv       = Nv
  
)


# Condiciones iniciales del sistema
xstart <- c(Sh = VALOR?,        # COMPLETE 
            Ih = VALOR?,        # COMPLETE
            Rh = VALOR?,        # COMPLETE
            Sv = VALOR?,        # COMPLETE
            Ev = VALOR?,        # COMPLETE
            Iv = VALOR?)        # COMPLETE

# Resuelva las ecuaciones
out <- as.data.frame(ode(y      = ARGUMENTO?,   # COMPLETE
                         times  = ARGUMENTO?,   # COMPLETE
                         fun    = ARGUMENTO?,   # COMPLETE
                         parms  = ARGUMENTO?))  # COMPLETE

Resultados

Para tener una visualización más significativa de los resultados, convierta las unidades de tiempo días en años y en semanas.

# Cree las opciones de tiempo a mostrar 
out$years <- 
out$weeks <-

Comportamiento General (Población humana)

# Revise el comportamiento general del modelo para 100 años

p1h <- ggplot(data = out, aes(y = (Rh + Ih + Sh)/10000, x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población humana total') +
  theme_bw() + ylab('number per 10,000')

p2h <- ggplot(data = out, aes(y = Sh/10000, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('number per 10,000')

p3h <- ggplot(data = out, aes(y = Ih/10000, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infectada') +
  theme_bw() + ylab('number per 10,000')

p4h <- ggplot(data = out, aes(y = Rh/10000, x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('number per 10,000')


grid.arrange(p1h, p2h, p3h, p4h, ncol = 2)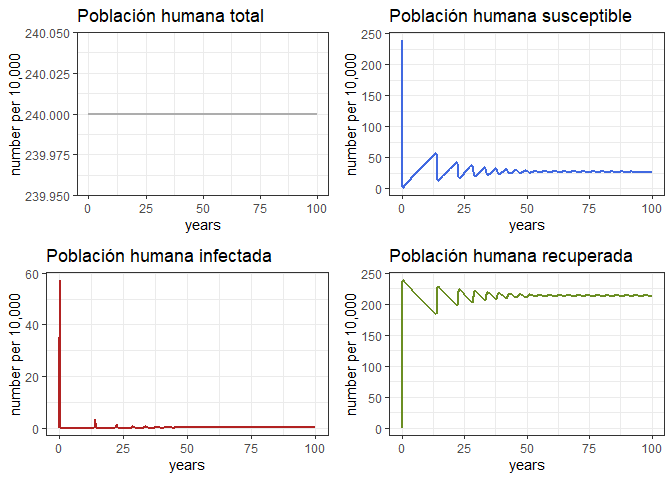

Comportamiento General (Población de vectores)

# Revise el comportamiento general del modelo

p1v <- ggplot(data = out, aes(y = (Sv + Ev + Iv), x = years)) +
  geom_line(color = 'grey68', size = 1) +
  ggtitle('Población total de mosquitos') +
  theme_bw() + ylab('number')

p2v <- ggplot(data = out, aes(y = Sv, x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población susceptible de mosquitos') +
  theme_bw() + ylab('number')

p3v <- ggplot(data = out, aes(y = Ev, x = years)) +
  geom_line(color = 'orchid', size = 1) +
  ggtitle('Población expuesta de mosquitos') +
  theme_bw() + ylab('number')

p4v <- ggplot(data = out, aes(y = Iv, x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población infectada de mosquitos') +
  theme_bw() + ylab('number')

grid.arrange(p1v, p2v, p3v, p4v, ncol = 2)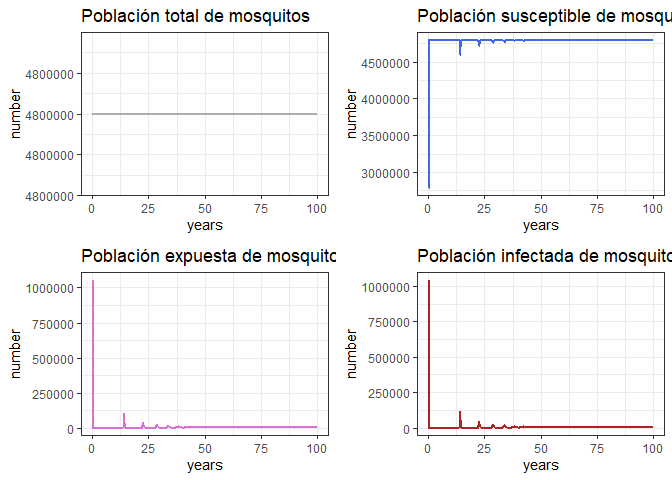

Proporción

Vamos a dar una mirada más cuidadosa a las proporciones y discutámoslas

p1 <- ggplot(data = out, aes(y = Sh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'royalblue', size = 1) +
  ggtitle('Población humana susceptible') +
  theme_bw() + ylab('proportion')

p2 <- ggplot(data = out, aes(y = Ih/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población humana infectada') +
  theme_bw() + ylab('proportion')

p3 <- ggplot(data = out, aes(y = Rh/(Sh+Ih+Rh), x = years)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('proportion')

grid.arrange(p1, p2, p3, ncol = 2)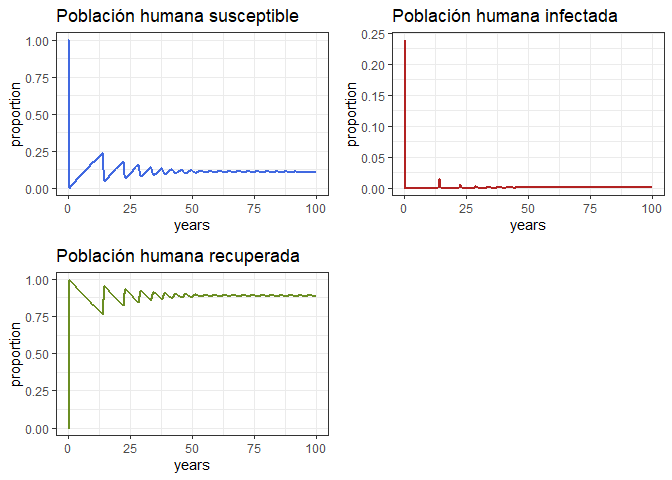

La primera epidemia

# Revise la primera epidemia

dat <- out[out$weeks < 54, ]

p1e <- ggplot(dat, aes(y = Ih/10000, x = weeks)) +
  geom_line(color = 'firebrick', size = 1) +
  ggtitle('Población de humanos infectados') +
  theme_bw() + ylab('número por 10,000')


p2e <- ggplot(dat, aes(y = Rh/10000, x = weeks)) +
  geom_line(color = 'olivedrab', size = 1) +
  ggtitle('Población humana recuperada') +
  theme_bw() + ylab('number per 10,000')


grid.arrange(p1e, p2e)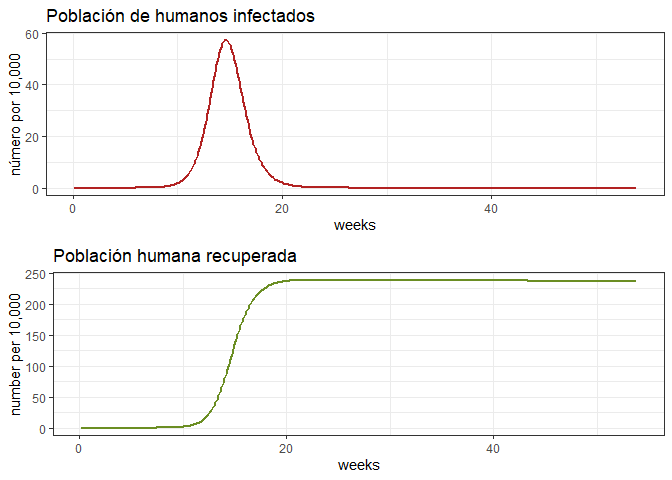

Discutamos algunos aspectos

Sensibilidad del modelo a cambios en $R_0$ .
¿Qué razones hay para el intervalo de tiempo entre epidemias?
¿Comó se calcula la tasa de ataque?

Modele la intervención control

Ahora, utilizando este modelo básico, vamos a modelar el impacto de tres tipos diferentes de intervenciones.

Vacunación
Mosquiteros/angeos
Fumigación contra mosquitos

Intente encontrar literatura que explique estas intervenciones y describa cómo parametrizará el modelo. ¿Todas estas intervenciones son viables? ¿Son rentables?

Sobre este documento

Contribuciones

Zulma Cucunuba & Pierre Nouvellet: Versión incial
Kelly Charinga & Zhian N. Kamvar: Edición
José M. Velasco-España: Traducción de Inglés a Español
Andree Valle-Campos: Ediciones menores

Contribuciones son bienvenidas vía pull requests. El archivo fuente de este documento puede ser encontrado aquí.