Una introducción a R y RStudio
Introducción
El presente tutorial es parte de los materiales de pre-curso “Curso corto sobre análisis y modelización de brotes para la salud pública.” El objetivo es presentar a los estudiantes los conceptos básicos de R y R Studio, con el fin de obtener algunos conocimientos básicos en la programación de R y R.
Instalando R y R Studio
R es un entorno de software libre y RStudio es un entorno gratuito y de código abierto para trabajar en R. Tanto R como RStudio deben instalarse por separado.
R se puede instalar desde el sitio web de R Project for Statistical computing (Proyecto R para la Estadística Computacional): https://r-project.org/
RStudio se puede instalar desde su sitio web. La versión gratuita es
suficiente para realizar análisis epidemiológicos de rutina.
https://www.rstudio.com/products/rstudio/download/
Una vez instalados ambos, trabaje desde RStudio.
Para obtener una explicación más detallada sobre cómo instalar R y RStudio, visite el video realizado por Thibaut Jombart de RECON https://www.youtube.com/watch?v=LbezGA_Yle8
Configuración del proyecto
Una de las grandes ventajas de usar RStudio es la posibilidad de usar
los Proyectos en R (R Project)(indicado por un archivo .Rproj) lo que
permite organizar el espacio de trabajo, el historial y los documentos
fuente.
Para crear un Proyecto en R, siga los siguientes pasos:
- Abra RStudio y en la esquina superior derecha, seleccione la pestaña File (Archivo) -> New Project… (Proyecto Nuevo).
- Se desplegará una ventana con encabezado New Project Wizard: Create Project, ahora seleccione New Directory (Directorio Nuevo).
- En la ventana Project Type, cree un nuevo proyecto en Rstudio seleccionando New Project -> Create New Project, en la casilla Directory Name (Nombre del Directorio) coloque el nombre “introR”.
- Seleccione el botón Browse…, ahora debe crear una carpeta que servira de repositorio para su proyecto, así como las sub carpetas que necesita para organizar su trabajo (por ejemplo: datos, scripts, figuras). Al final seleccione la carpeta que servira de repositorio.
Al final, su proyecto debería parecerse a esta imagen
Estructuras en R
Según Hadley Wickham, en su libro R Avanzado [http://adv-r.had.co.nz/], hay dos tipos de estruturas en R:
- Homogéneas: vectores (1d), matrices (2d) y arreglos (nd)
- Heterogéneas: marcos de datos y listas
Vectores
Estas son las estructuras más básicas en R y tienen solo una dimensión (1d):
- Vector Doble (numérico) vector_double
- Vector Lógico vector_logic
- Vector de caracteres vector_character
- Vector Entero vector_integer
vector_double <- c(1, 2, 3, 4)
vector_logic <- c(TRUE, FALSE, FALSE, TRUE)
vector_character<- c("A", "B", "C", "D")
vector_integer <- c(1L, 2L, 3L, 4L)Para evaluar qué tipo de vector tenemos, podemos usar el comando
typeof
typeof(vector_double)
## [1] "double"
typeof(vector_logic)
## [1] "logical"
typeof(vector_character)
## [1] "character"
typeof(vector_integer)
## [1] "integer"Matrices
Las matrices son estructuras un poco más complejas que los vectores, con dos caracteristicas principales:
- Una matriz esta compuesta de solo un tipo de vector
- Un matriz tiene dos dimensiones
Un comando para construir una matrix (Matriz) usa tres argumentos:
datacorresponde a la lista de vectores que queremos usar en la matriznrowel número de filas donde se dividirán los datos (primera dimensión)ncolel número de columnas donde se dividirán los datos (segunda dimensión)
Por defecto, la matriz se llena por columnas, a menos que especifiquemos
lo contrario usando byrow = TRUE
matrix_of_doub <- matrix(data = vector_double, nrow = 2, ncol = 2)
matrix_of_doub
## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
dim(matrix_of_doub)
## [1] 2 2Para hacer y probar otros tipos de matrices
matrix_of_log <- matrix(data = vector_logic, nrow = 4, ncol = 3)
matrix_of_log
matrix_of_char <- matrix(data = vector_character, nrow = 4, ncol = 4)
matrix_of_char
matrix_of_int <- matrix(data = vector_integer, nrow = 4, ncol = 5)
matrix_of_intArreglos multidimensionales
Los arreglos multidimensionales(Array) son un tipo especial de matriz, donde hay más de dos dimensiones (n dimensiones).
Un arreglo de dos dimensiones es una matriz
Para crear un arreglo multidimensional(Array), se necesitan los
argumentos: data y dim.
A su vez, el dim de un arreglo esta compuesto de tres argumentos: 1)
número de filas, 2) números de columnas y 3) número de dimensiones.
vector_example <-1:18
array_example <- array(data = vector_example, dim = c(2, 3, 3))
dim(array_example)
## [1] 2 3 3
array_example
## , , 1
##
## [,1] [,2] [,3]
## [1,] 1 3 5
## [2,] 2 4 6
##
## , , 2
##
## [,1] [,2] [,3]
## [1,] 7 9 11
## [2,] 8 10 12
##
## , , 3
##
## [,1] [,2] [,3]
## [1,] 13 15 17
## [2,] 14 16 18Marco de datos (Data frames)
Un data.frame (marco de datos) es una estructura heterogénea y
bidimensional, similar pero no exactamente igual a una matriz. A
diferencia de una matriz, varios tipos de vectores pueden formar parte
de un solo marco de datos.
Los argumentos para el comando data.frame (marco de datos) son
simplemente las columnas en el marco de datos. Cada columna debe tener
el mismo número de filas para poder caber en un marco de datos.
Los marcos de datos no permiten vectores con diferentes longitudes. Cuando la longitud del vector es menor que la longitud del marco de datos, el marco de datos fuerza al vector a su longitud.
data_example <- data.frame(vector_character, vector_double, vector_logic, vector_integer)Para acceder a la estructura general de un marco de datos usamos el
comando str
str(data_example)
## 'data.frame': 4 obs. of 4 variables:
## $ vector_character: chr "A" "B" "C" "D"
## $ vector_double : num 1 2 3 4
## $ vector_logic : logi TRUE FALSE FALSE TRUE
## $ vector_integer : int 1 2 3 4Para acceder a los diferentes componentes del marco de datos usamos esta
sintaxis [,] donde la primera dimensión corresponde a filas y la
segunda dimensión a columnas.
data_example[1, 2]
## [1] 1Listas
Una list (lista) es la estructura más compleja en las bases de R. Una
lista puede estar compuesta por cualquier tipo de objetos de cualquier
dimensión.
list_example <- list(vector_character,
matrix_of_doub,
data_example)Para acceder a los diferentes componentes de una lista, usamos la
sintaxis [] donde el argumento es simplemente el orden dentro de la
lista.
list_example[1]
## [[1]]
## [1] "A" "B" "C" "D"Funciones
Una función es una de las estructuras que hace de * R * una plataforma muy potente para la programación.
Hay varios tipos de funciones:
- Funciones básicas o primitivas: estas son las funciones
predeterminadas en R bajo el base package (paquete base). Por
ejemplo, pueden incluir operaciones aritméticas básicas, pero
también operaciones más complejas como la extracción de valores
medianos
median (mediana)osummary (resumen)de una variable.- Funciones de paquetes: son funciones creadas dentro de un
paquete. Por ejemplo, la función
glmen el paquete stats (stats package). - Funciones creadas por el usuario: son funciones que cualquier usuario crea para una rutina personalizada. Estas funciones podrían formar parte de un paquete.
- Funciones de paquetes: son funciones creadas dentro de un
paquete. Por ejemplo, la función
Los componentes basicos de una función son:
- name (nombre): es el nombre que se da a la función(Por ejemplo:
myfun) - formals (argumentos): son la serie de elementos que controlan cómo llamar a la función.
- body (cuerpo): es la serie de operaciones o modificaciones a los argumentos.
- output (salida o resultado): son los resultados después de
modificar los argumentos. Si esta salida corresponde a una serie de
datos, podemos extraerla usando el comando
return. - internal function enviroment (ambiente interno de la función): son las reglas y objetos específicos dentro de una función. Esas reglas y objetos no funcionarán fuera de la función.
Función creada por el usuario (ejemplo 1)
Para crear una función que calcula el Indice de Masa Corporal (IMC o BMI por sus siglas en inglés)
# Inicialmente poner el nombre a la función (ej. myfun)
myfun <- function(weight,
height) # Los argumentos (weight (Peso) and height (Talla))
{
# Ahora escribir el cuerpo de la función
BMI <- weight/(height^2)
return(BMI) # Finalmente se usa este comando para generar la salida
}
#Para conocer los argumentos de la función usar
formals(myfun)
## $weight
##
##
## $height
#Para conocer el cuerpo de la función usar
body(myfun)
## {
## BMI <- weight/(height^2)
## return(BMI)
## }
#Para conocer el ambiente de la función usar
environment(myfun)
## <environment: R_GlobalEnv>
#Para utilizar la función
#Se escribe la función y se asigna valores a cada argumento
myfun(weight = 88, height = 1.78)
## [1] 27.77427Función creada por el usuario (ejemplo 2)
Ahora se creará una función con argumentos predeterminados. De esta forma, no se necesita especificar algunos argumentos al usar la función.
# Inicialmente poner el nombre a la función(ej. myfun2)
myfun2 <- function(weight,
height,
units = 'kg/m2') # Los argumentos (weight and height)
{
# Ahora escribir el cuerpo de la función
BMI <- weight/(height^2)
output <- paste(round(BMI, 1), units)
return(output) # Finalmente se usa este comando para generar la salida
}
#Ahora se escribe la función y se asigna valores a cada argumento
#El resultado tendrá incluido el argumento units
myfun2(weight = 88, height = 1.78)
## [1] "27.8 kg/m2"
#Ahora bien si se quiere cambiar el argumento predeterminado es posible
#Se asigna valores a cada argumento incluyendo el predeterminado
myfun2(weight = 8800, height = 178, units = 'g/cm2')
## [1] "0.3 g/cm2"R packages (Paquetes de R)
Como lo describe Hadley Wickham en su libro R packages, un paquete es la unidad fundamental para reproducir el código en R. Un paquete debe incluir al menos: - Funciones R reutilizables - documentación - Datos de muestra
Cualquier usuario de R puede crear un paquete que luego otros usuarios pueden usar o modificar, ya que son de código abierto.
Los paquetes R están disponibles en el Comprehensive R Archive Network (CRAN) https://cran.r-project.org
Estos son los comandos básicos para usar paquetes:
- Para instalar un paquete, se usa el
comando
install.packages("package-name") - Para cargarlos en R, se usar el comando
library("package-name")
Para instalar y cargar un paquete de RECON, escribir en R
install.packages('incidence')library(incidence)La biblioteca es un directorio que contiene los paquetes instalados.
Para verificar que paquetes están activos actualmente en la sesión de R,
se utiliza el comando lapply(.libPaths(), dir).
Una parte importante de un paquete es la documentación. Esto se almacena
en las vignettes. Para acceder a la documentación básica de un
paquete, se usa el comando browseVignettes("incidence")
Alcance y Entornos
Se crea un nuevo entorno cuando creamos una función. ¡Esto es importante! Cuando llamamos a una función, R primero busca los elementos dentro de esa función; si los elementos no existen dentro de esa función, entonces R los busca en el entorno global.
- Ejemplo de una función en la que todos los objetos están disponibles solo en el entorno global
mynewfun <- function() {
z = x + y
return(z)
}
x = 1
y = 3
mynewfun()
## [1] 4- Ejemplo de una función en la que los objetos estan parcialmente en el entorno local y parcialmente en el entorno global
mynewfun <- function(xx) {
zz = xx + yy
return(zz)
}
yy = 4
mynewfun(xx = 4)
## [1] 8Esta característica de R es muy importante al ejecutar cualquier análisis o rutina. Siempre se recomienda NO utilizar elementos dentro de una función que solo estén disponibles en el entorno global.
Crear y abrir conjuntos de datos
R permite a los usuarios no solo abrir, sino también crear conjuntos de datos. Hay tres fuentes de conjuntos de datos:
- Conjunto de datos importado (desde los formatos
.xlsx,.csv,.stata, o.RDS, entre otros) - Conjunto de datos que forma parte de un paquete en R
- Conjunto de datos creado durante la sesión en R
Tidyverse
Para administrar mejor los conjuntos de datos, se recomienda instalar y
usar el paquete tidyverse, el cual carga automáticamente varios
paquetes (dplyr, tidyr, tibble, readr, purr, entre otros) que son útiles
para la manipulación de datos.
install.packages('tidyverse')library(tidyverse)Abrir y explorar un conjunto de datos importados de Excel
Este es el conjunto de datos para esta práctica de RECON sobre análisis temprano de brotes: - PHM-EVD-linelist-2017-11-25.xlsx:
Dentro del directorio en el que está trabajando actualmente, cree una carpeta llamada data. Guarde el conjunto de datos descargado en la carpeta data que acaba de crear.
Para importar conjuntos de datos desde Excel, se puede usar la
biblioteca readxl, que está vinculada a tidyverse. Sin embargo,
todavía es necesario cargar la biblioteca readxl, ya que no es un
paquete tidyverse principal.
library(readxl)
dat <- read_excel("data/PHM-EVD-linelist-2017-11-25.xlsx")A continuación, verá algunas de las funciones más utilizadas de
tidyverse.
La función de tubería (pipe function) %>% es una función de uso
continuo. Por lo que es clave para usar tidyverse y facilita la
programación. La función de tubería permite al usuario enfatizar una
secuencia de acciones en un objeto.
Del paquete dyplr, las funciones más comunes son:
glimpse: utilizado para explorar rápidamente un conjunto de datosselect: extrae columnas de un conjunto de datosfilter: extrae filas de un conjunto de casosarrange: ordena filas de un conjunto de datos por el valor de una variable particular si es numérico, o por orden alfabético si es un carácter.summarise: genera tablas resumen. reduce las dimensiones de un conjunto de datosgroup_by: crea grupos dentro de un conjunto de datos. las funciones deldplyrmanipulan cada grupo por separado y luego combina los resultados.mutate: genera una nueva variablerename: cambia el nombre de la variable
dat %>% glimpse()
## Rows: 50
## Columns: 4
## $ case_id <chr> "39e9dc", "664549", "b4d8aa", "51883d", "947e40", "9aa197", "e~
## $ onset <dttm> 2017-10-10, 2017-10-16, 2017-10-17, 2017-10-18, 2017-10-20, 2~
## $ sex <chr> "female", "male", "male", "male", "female", "female", "female"~
## $ age <dbl> 62, 28, 54, 57, 23, 66, 13, 10, 34, 11, 23, 23, 9, 68, 37, 13,~
dat %>% select(onset)
## # A tibble: 50 x 1
## onset
## <dttm>
## 1 2017-10-10 00:00:00
## 2 2017-10-16 00:00:00
## 3 2017-10-17 00:00:00
## 4 2017-10-18 00:00:00
## 5 2017-10-20 00:00:00
## 6 2017-10-20 00:00:00
## 7 2017-10-21 00:00:00
## 8 2017-10-21 00:00:00
## 9 2017-10-21 00:00:00
## 10 2017-10-22 00:00:00
## # ... with 40 more rows
dat %>% filter(age >14)
## # A tibble: 34 x 4
## case_id onset sex age
## <chr> <dttm> <chr> <dbl>
## 1 39e9dc 2017-10-10 00:00:00 female 62
## 2 664549 2017-10-16 00:00:00 male 28
## 3 b4d8aa 2017-10-17 00:00:00 male 54
## 4 51883d 2017-10-18 00:00:00 male 57
## 5 947e40 2017-10-20 00:00:00 female 23
## 6 9aa197 2017-10-20 00:00:00 female 66
## 7 185911 2017-10-21 00:00:00 female 34
## 8 605322 2017-10-22 00:00:00 female 23
## 9 e399b1 2017-10-23 00:00:00 female 23
## 10 f658bc 2017-10-28 00:00:00 male 68
## # ... with 24 more rows
dat %>% filter(sex == "female", age <= 30)
## # A tibble: 19 x 4
## case_id onset sex age
## <chr> <dttm> <chr> <dbl>
## 1 947e40 2017-10-20 00:00:00 female 23
## 2 e4b0a2 2017-10-21 00:00:00 female 13
## 3 605322 2017-10-22 00:00:00 female 23
## 4 e399b1 2017-10-23 00:00:00 female 23
## 5 e37897 2017-10-28 00:00:00 female 9
## 6 8c5776 2017-11-02 00:00:00 female 7
## 7 88526e 2017-11-03 00:00:00 female 20
## 8 778316 2017-11-04 00:00:00 female 10
## 9 525dfa 2017-11-06 00:00:00 female 10
## 10 b5ad13 2017-11-07 00:00:00 female 21
## 11 8bed66 2017-11-08 00:00:00 female 29
## 12 426b6d 2017-11-08 00:00:00 female 7
## 13 c2a389 2017-11-10 00:00:00 female 26
## 14 5eb2b0 2017-11-13 00:00:00 female 7
## 15 b7faf4 2017-11-16 00:00:00 female 10
## 16 944ba3 2017-11-19 00:00:00 female 30
## 17 95fc1d 2017-11-19 00:00:00 female 15
## 18 5c5c05 2017-11-20 00:00:00 female 21
## 19 ac8d9d 2017-11-23 00:00:00 female 5
dat %>% arrange(age)
## # A tibble: 50 x 4
## case_id onset sex age
## <chr> <dttm> <chr> <dbl>
## 1 ac8d9d 2017-11-23 00:00:00 female 5
## 2 8c5776 2017-11-02 00:00:00 female 7
## 3 426b6d 2017-11-08 00:00:00 female 7
## 4 93a3ba 2017-11-10 00:00:00 male 7
## 5 5eb2b0 2017-11-13 00:00:00 female 7
## 6 1efd54 2017-11-04 00:00:00 male 8
## 7 e37897 2017-10-28 00:00:00 female 9
## 8 59e66c 2017-11-16 00:00:00 male 9
## 9 af0ac0 2017-10-21 00:00:00 male 10
## 10 778316 2017-11-04 00:00:00 female 10
## # ... with 40 more rows
dat %>% summarise(number = n())
## # A tibble: 1 x 1
## number
## <int>
## 1 50
dat %>% group_by(sex) %>% summarise(number = n(), mean_age = mean(age))
## # A tibble: 2 x 3
## sex number mean_age
## <chr> <int> <dbl>
## 1 female 26 23.7
## 2 male 24 24.5
dat %>% mutate(fecha_inicio_sintomas = onset)
## # A tibble: 50 x 5
## case_id onset sex age fecha_inicio_sintomas
## <chr> <dttm> <chr> <dbl> <dttm>
## 1 39e9dc 2017-10-10 00:00:00 female 62 2017-10-10 00:00:00
## 2 664549 2017-10-16 00:00:00 male 28 2017-10-16 00:00:00
## 3 b4d8aa 2017-10-17 00:00:00 male 54 2017-10-17 00:00:00
## 4 51883d 2017-10-18 00:00:00 male 57 2017-10-18 00:00:00
## 5 947e40 2017-10-20 00:00:00 female 23 2017-10-20 00:00:00
## 6 9aa197 2017-10-20 00:00:00 female 66 2017-10-20 00:00:00
## 7 e4b0a2 2017-10-21 00:00:00 female 13 2017-10-21 00:00:00
## 8 af0ac0 2017-10-21 00:00:00 male 10 2017-10-21 00:00:00
## 9 185911 2017-10-21 00:00:00 female 34 2017-10-21 00:00:00
## 10 601d2e 2017-10-22 00:00:00 male 11 2017-10-22 00:00:00
## # ... with 40 more rows
dat %>% rename(edad = age)
## # A tibble: 50 x 4
## case_id onset sex edad
## <chr> <dttm> <chr> <dbl>
## 1 39e9dc 2017-10-10 00:00:00 female 62
## 2 664549 2017-10-16 00:00:00 male 28
## 3 b4d8aa 2017-10-17 00:00:00 male 54
## 4 51883d 2017-10-18 00:00:00 male 57
## 5 947e40 2017-10-20 00:00:00 female 23
## 6 9aa197 2017-10-20 00:00:00 female 66
## 7 e4b0a2 2017-10-21 00:00:00 female 13
## 8 af0ac0 2017-10-21 00:00:00 male 10
## 9 185911 2017-10-21 00:00:00 female 34
## 10 601d2e 2017-10-22 00:00:00 male 11
## # ... with 40 more rows
dat %>% slice(10:15)
## # A tibble: 6 x 4
## case_id onset sex age
## <chr> <dttm> <chr> <dbl>
## 1 601d2e 2017-10-22 00:00:00 male 11
## 2 605322 2017-10-22 00:00:00 female 23
## 3 e399b1 2017-10-23 00:00:00 female 23
## 4 e37897 2017-10-28 00:00:00 female 9
## 5 f658bc 2017-10-28 00:00:00 male 68
## 6 a8e9d8 2017-10-29 00:00:00 female 37
dat[10:15, ]
## # A tibble: 6 x 4
## case_id onset sex age
## <chr> <dttm> <chr> <dbl>
## 1 601d2e 2017-10-22 00:00:00 male 11
## 2 605322 2017-10-22 00:00:00 female 23
## 3 e399b1 2017-10-23 00:00:00 female 23
## 4 e37897 2017-10-28 00:00:00 female 9
## 5 f658bc 2017-10-28 00:00:00 male 68
## 6 a8e9d8 2017-10-29 00:00:00 female 37Ahora, se abrirá y explorará un conjunto de datos que forma parte de un paquete
install.packages("outbreaks")library(outbreaks)
## Warning: package 'outbreaks' was built under R version 4.0.5
measles_dat <- outbreaks::measles_hagelloch_1861
class(measles_dat)
## [1] "data.frame"
head(measles_dat)
## case_ID infector date_of_prodrome date_of_rash date_of_death age gender
## 1 1 45 1861-11-21 1861-11-25 <NA> 7 f
## 2 2 45 1861-11-23 1861-11-27 <NA> 6 f
## 3 3 172 1861-11-28 1861-12-02 <NA> 4 f
## 4 4 180 1861-11-27 1861-11-28 <NA> 13 m
## 5 5 45 1861-11-22 1861-11-27 <NA> 8 f
## 6 6 180 1861-11-26 1861-11-29 <NA> 12 m
## family_ID class complications x_loc y_loc
## 1 41 1 yes 142.5 100.0
## 2 41 1 yes 142.5 100.0
## 3 41 0 yes 142.5 100.0
## 4 61 2 yes 165.0 102.5
## 5 42 1 yes 145.0 120.0
## 6 42 2 yes 145.0 120.0
tail(measles_dat)
## case_ID infector date_of_prodrome date_of_rash date_of_death age gender
## 183 183 184 1861-11-11 1861-11-15 <NA> 4 m
## 184 184 NA 1861-10-30 1861-11-06 <NA> 13 <NA>
## 185 185 82 1861-12-03 1861-12-07 <NA> 3 m
## 186 186 45 1861-11-22 1861-11-26 <NA> 6 <NA>
## 187 187 82 1861-12-07 1861-12-11 <NA> 0 m
## 188 188 175 1861-11-23 1861-11-27 <NA> 1 <NA>
## family_ID class complications x_loc y_loc
## 183 4 0 yes 182.5 200.0
## 184 51 2 yes 182.5 200.0
## 185 21 0 yes 205.0 182.5
## 186 57 0 yes 212.5 90.0
## 187 21 0 yes 205.0 182.5
## 188 57 0 yes 212.5 90.0
measles_dat %>% select(starts_with("date_")) %>% head()
## date_of_prodrome date_of_rash date_of_death
## 1 1861-11-21 1861-11-25 <NA>
## 2 1861-11-23 1861-11-27 <NA>
## 3 1861-11-28 1861-12-02 <NA>
## 4 1861-11-27 1861-11-28 <NA>
## 5 1861-11-22 1861-11-27 <NA>
## 6 1861-11-26 1861-11-29 <NA>Del paquetetidyr, las funciones más comunes son:
pivot_longer: apila en filas datos dispersos en columnas. Es una versión actualizada degatherpivot_wider: dispersa en columnas datos apilados. Es una versión actualizada despread
Ejemplo:
# crear base de datos en formato "wide"
malaria_wide <- tibble(
district = rep(letters[1:5],each = 2),
gender = rep(c('f', 'm'), 5),
falciparum = round(rnorm(10, 30, 10), 0),
vivax = round(rnorm(10, 30, 10), 0)
)
malaria_wide
## # A tibble: 10 x 4
## district gender falciparum vivax
## <chr> <chr> <dbl> <dbl>
## 1 a f 34 30
## 2 a m 33 33
## 3 b f 19 40
## 4 b m 26 35
## 5 c f 28 39
## 6 c m 26 40
## 7 d f 32 29
## 8 d m 8 50
## 9 e f 26 28
## 10 e m 25 25
# transformar base "wide" a formato "long"
malaria_long <- malaria_wide %>%
pivot_longer(falciparum:vivax, names_to = "infection", values_to = "cases")
malaria_long
## # A tibble: 20 x 4
## district gender infection cases
## <chr> <chr> <chr> <dbl>
## 1 a f falciparum 34
## 2 a f vivax 30
## 3 a m falciparum 33
## 4 a m vivax 33
## 5 b f falciparum 19
## 6 b f vivax 40
## 7 b m falciparum 26
## 8 b m vivax 35
## 9 c f falciparum 28
## 10 c f vivax 39
## 11 c m falciparum 26
## 12 c m vivax 40
## 13 d f falciparum 32
## 14 d f vivax 29
## 15 d m falciparum 8
## 16 d m vivax 50
## 17 e f falciparum 26
## 18 e f vivax 28
## 19 e m falciparum 25
## 20 e m vivax 25
# transformar base "long" a formato "wide"
malaria_long %>%
pivot_wider(names_from = infection, values_from = cases)
## # A tibble: 10 x 4
## district gender falciparum vivax
## <chr> <chr> <dbl> <dbl>
## 1 a f 34 30
## 2 a m 33 33
## 3 b f 19 40
## 4 b m 26 35
## 5 c f 28 39
## 6 c m 26 40
## 7 d f 32 29
## 8 d m 8 50
## 9 e f 26 28
## 10 e m 25 25
# versiones equivalentes usando gather() y spread()
# malaria_wide %>% gather(key = "infection", value = "cases",falciparum:vivax)
# malaria_long %>% spread(key = infection, value = cases)ggplot2
ggplot es una implementación del concepto de gramática de gráficos
que ha sido implementado en R por Hadley Wickham. Hadley explica en su
libro ggplot2 que “la gramática es un mapeo desde los datos a atributos
estéticos (color, forma, tamaño) para objetos geométricos (puntos,
líneas, barras)”.
Los componentes principales de un gráfico ggplot2 son:
- data frame (marco de datos)
- aesthesic mappings (mapeos estéticos) se refiere a las indicaciones sobre cómo se deben asignar los datos (x, y) al color, tamaño, etc.
- geoms (geometría) se refiere a objetos geométricos como puntos, líneas, formas
- facets (facetas) para gráficos condicionales
- coordinates system (sistema de coordenadas)
Funciones básicas en ggplot
ggplot() es la función núcleo en ggplot2. El argumento básico de la
función es el marco de datos que queremos graficar. ggplot(data) se
puede unir a otros tipos de funciones usando el símbolo +, como por
ejemplo a las geoms. Algunos de los más utilizados son:
geom_point(): para puntosgeom_line(): para lineasgeom_bar(): para graficas de barrasgeom_histogram(): para histogramas
Todos estos comandos utilizarán la misma sintaxis para la estética
(x, y, colour, fill, shape).
Ejemplo de GGplot con el conjunto de datos sobre sarampión
A continuación, se usará el conjunto de datos de sarampión del paquete
outbreaks que se importó anteriormente. En este caso, se hará un
gráfico que muestre la serie temporal de casos por semana y será
coloreada por género. Para lo cuál se define:
x= tiempoy= número agregado de casos por semana y génerocolour= género
Una cosa importante a tener en cuenta es que para una sola instrucción, ggplot solo usará variables que pertenezcan al mismo conjunto de datos. Entonces, necesitamos tener las tres variables (x, y, colour) en el mismo marco de datos (con la misma longitud).
head(measles_dat, 5)
## case_ID infector date_of_prodrome date_of_rash date_of_death age gender
## 1 1 45 1861-11-21 1861-11-25 <NA> 7 f
## 2 2 45 1861-11-23 1861-11-27 <NA> 6 f
## 3 3 172 1861-11-28 1861-12-02 <NA> 4 f
## 4 4 180 1861-11-27 1861-11-28 <NA> 13 m
## 5 5 45 1861-11-22 1861-11-27 <NA> 8 f
## family_ID class complications x_loc y_loc
## 1 41 1 yes 142.5 100.0
## 2 41 1 yes 142.5 100.0
## 3 41 0 yes 142.5 100.0
## 4 61 2 yes 165.0 102.5
## 5 42 1 yes 145.0 120.0A partir del comando anterior, puede notarse que el conjunto de datos de
sarampión no contiene actualmente una de las tres variables, la variable
y (número agregado de casos por semana y por género). Esto significa
que primero se debe modificar el marco de datos para que contenga las
tres variables que queremos graficar.
Para modificar el marco de datos, se puede usar varias funciones
explicadas anteriormente sobre el paquete dplyr.
measles_grouped <- measles_dat %>%
filter(!is.na(gender)) %>%
group_by(date_of_rash, gender) %>%
summarise(cases = n())
## `summarise()` has grouped output by 'date_of_rash'. You can override using the `.groups` argument.
head(measles_grouped, 5)
## # A tibble: 5 x 3
## # Groups: date_of_rash [4]
## date_of_rash gender cases
## <date> <fct> <int>
## 1 1861-11-03 m 1
## 2 1861-11-08 f 1
## 3 1861-11-11 f 1
## 4 1861-11-11 m 1
## 5 1861-11-13 m 1Una vez que el marco de datos está listo, gráficar es fácil:
ggplot(data = measles_grouped) +
geom_line(aes(x = date_of_rash, y = cases, colour = gender))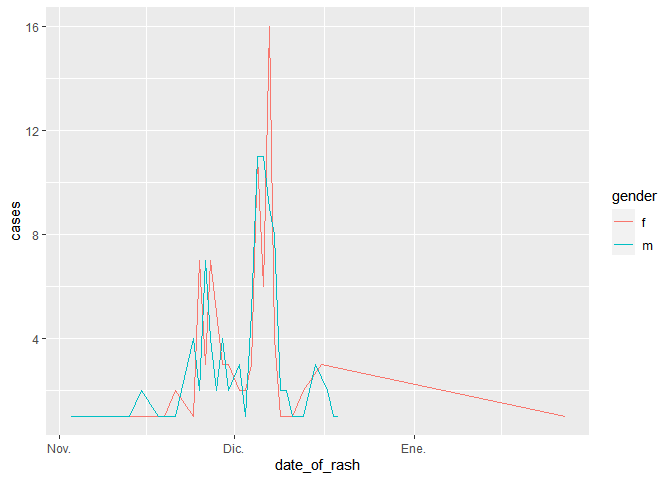
Por defecto, ggplot toma varias decisiones por si solo, como los colores utilizados, el tamaño de las líneas, el tamaño de la fuente, etc. En ocasiones, es posible que se quiera cambiarlos para mejorar la presentación de los datos.
En seguida se muestra una forma alternativa de presentar los mismos datos. Modifique algunas de las líneas y observe cómo cambia el gráfico.
p <- ggplot(data = measles_grouped,
aes(x = date_of_rash, y = cases, fill = gender)) +
geom_bar(stat = 'identity', colour = 'black', alpha = 0.5) +
facet_wrap(~ gender, nrow = 2) +
xlab('Date of onset') +
ylab('measles cases') +
ggtitle('Measles Cases in Hagelloch (Germany) in 1861') +
theme(strip.background = element_blank(),
strip.text.x = element_blank()) +
theme(legend.position = c(0.9, 0.2)) +
scale_fill_manual(values =c('purple', 'green'))
p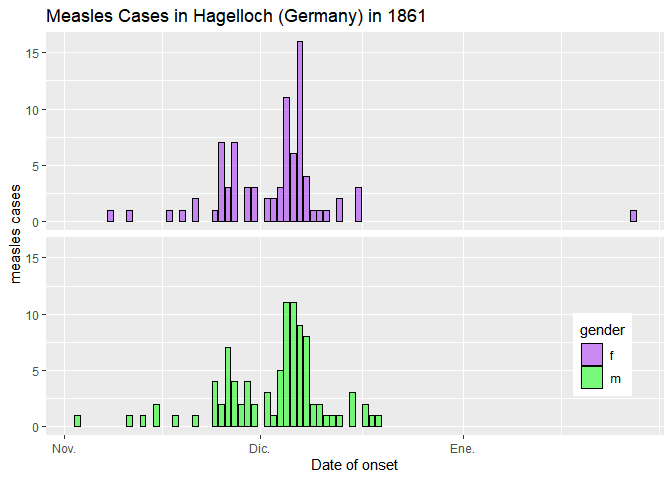
Finalmente, ggplot tiene una función útil que permite a los usuarios agregar capas sobre los objetos existentes de ggplot. Por ejemplo, si se quiere cambiar el título y el color de la variable de género después de terminar el gráfico, no es necesario volver a hacer el gráfico. Simplemente se agrega un comando para sobrescribir el gráfico anterior.
p +
ggtitle('another title') +
scale_fill_manual(values =c('blue', 'lightblue'))
## Scale for 'fill' is already present. Adding another scale for 'fill', which
## will replace the existing scale.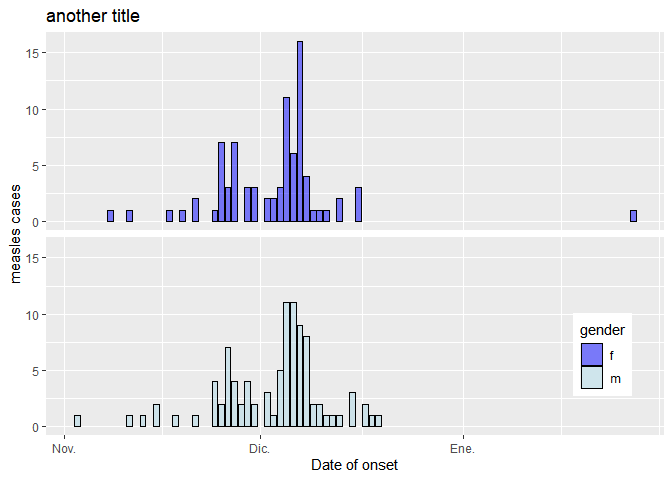
Trabajar con distribuciones de probabilidad
Todas las distribuciones en R se pueden explorar mediante el uso de funciones que nos permiten obtener diferentes formas de distribución. Afortunadamente, todas las distribuciones funcionan de la misma manera, por lo que si aprende a trabajar con una, tendrá la idea general de cómo trabajar con las demás.
Por ejemplo, para una distribución normal se usa dnorm. Puedes usar
?dnorm para explorar los argumentos en esta función:
dnorm(x, mean = 0, sd = 1, log = FALSE) y sus funciones relacionadas:
dnormda la función de densidadpnormda la función de probabilidadqnormda la función cuantilrnormgenera valores aleatorios
Muchas distribuciones son parte del paquete stats que viene por
defecto con R, como uniform, poisson y binomial, entre otros. Para
otras distribuciones que se utilizan con menos frecuencia, a veces puede
que necesite instalar otros paquetes. Para obtener una lista no
exhaustiva de las distribuciones más utilizadas y sus argumentos,
consultar la siguiente tabla:
| Nombre | probabilidad | cuantil | distribución | random |
|---|---|---|---|---|
| Beta | pbeta() |
qbeta() |
dbeta() |
rbeta() |
| Binomial | pbinom() |
qbinom() |
dbinom() |
rbinom() |
| Cauchy | pcauchy() |
qcauchy() |
dcauchy() |
rcauchy() |
| Chi-Square | pchisq() |
qchisq() |
dchisq() |
rchisq() |
| Exponential | pexp() |
qexp() |
dexp() |
rexp() |
| Gamma | pgamma() |
qgamma() |
dgamma() |
rgamma() |
| Logistic | plogis() |
qlogis() |
dlogis() |
rlogis() |
| Log Normal | plnorm() |
qlnorm() |
dlnorm() |
rlnorm() |
| Negative Binomial | pnbinom() |
qnbinom() |
dnbinom() |
rnbinom() |
| Normal | pnorm() |
qnorm() |
dnorm() |
rnorm() |
| Poisson | ppois() |
qpois() |
dpois() |
rpois() |
| Student’s t | pt() |
qt() |
dt() |
rt() |
| Uniform | punif() |
qunif() |
dunif() |
runif() |
| Weibull | pweibull() |
qweibull() |
dweibull() |
rweibull() |
Uso de las funciones
rnorm()
Podemos ilustrar una distribución normal con media 0 y desviación estandar 1 dibujando un histograma con 1000 observaciones aleatorias a partir de esta distribución.
hist(rnorm(n = 1000))Cada vez que corras esta última línea, generaras un nuevo conjunto de datos aleatorios. ¡Inténtalo!
dnorm()
La densidad de la distribución aleatoria a cualquier punto dado indica qué tan probable son dichos valores en dicho rango.
dnorm(x = 0)
dnorm(x = -1)
dnorm(x = 1)Tal y como vemos en la gráfica anterior tanto 1 como -1 tienen una densidad muy similar
¿Cuál es el valor de la densidad para un valor poco probable en el rango, por ejemplo 4?
dnorm(x = 4)pnorm()
Los valores de densidad no proveen los valores de la probabildiad, pero dan una idea de su probabilidad relativa.
El percentil proporciona información sobre la probabilidad de que los valores de una distribución normal caigan por debajo de un valor determinado.
¿Cuál es la probabilidad de que los valores sean inferiores a -1?
pnorm(q = -1)¿Cuál es la probabilidad de que los valores sean inferiores a 0? o, ¿Qué proporción de valores cae por debajo de 0?
pnorm(q = 0)¿Qué proporción de valores cae por debajo de 1?
pnorm(q = 1)En análisis estadísticos, una distribución normal puede ser usada para representar potenciales observaciones debajo de una hipótesis nula. Si una observación cae lejos en las colas de esta distribución, sugiere que podemos rechazar la hipótesis nula.
Para una distribución normal, ¿Cuál es la probabilidad de que una observación caiga debajo de -1.96?
pnorm(q = -1.96)¿Cuál es la probabilidad de que una observación caiga por arriba de 1.96?
1 - pnorm(q = 1.96)Note que estos valores son frecuentemente usados como punto de corte, de
forma que la probabilidad de una observación caiga debajo de -1.96 o
arriba de 1.96, sumando aproximadamente 0.05.
pnorm(q = -1.96) + (1 - pnorm(q = 1.96))0.05 representa una probabilidad aceptablemente baja de que un valor
extremo pueda ser observado en una muestra si la hipótesis nula es
correcta.
qnorm()
La función cuantil permite plantear preguntas diferentes pero relacionadadas, Por ejemplo: ¿Por debajo de qué valor cae la mitad de la distribución?
qnorm(p = 0.5)¿Por debajo de qué valor cae el 2.5% de la distribución?
qnorm(p = 0.025)¿Por arriba de qué valor cae el 2.5% de la distribución?
qnorm(p = (1-0.025))Uso de los parámetros
Puedes realizar ejercicios similares con el resto de distribuciones usando las funciones de la tabla de arriba
Sin embargo, casi todas las distribuciones estadísticas emplean parámetros diferentes, por lo que sus funciones también requieren de diferentes argumentos.
Con el aplicativo web titulado “el zoológico de distribuciones” puedes explorar de forma interactiva varias distribuciones y sus respectivos parámetros. Revísalo aquí: https://ben18785.shinyapps.io/distribution-zoo/
Por ejemplo, la distribución binomial tiene dos parámetros, la
probabilidad de éxito, prob, y el número de ensayos, size.
La distribución binomial se suele ilustrar con una serie de lanzamientos
de una moneda, en la que el éxito puede definirse en términos de que el
lanzamiento de la moneda dé “cara”, y en la que prob = 0.5 si la
moneda es justa.
La distribución binomial sólo puede tomar valores enteros no negativos, a diferencia de la distribución normal, que incluye cualquier número entre -∞ y ∞.
hist(rbinom(n=100000, size=10, prob=0.5))Uso de las distribuciones estadísticas en epidemiología
Ejemplo 1
Podemos usar la distribución binomial para describir el número de
personas infectadas en un área muestreada. Por ejemplo, si muestreamos
un área que contiene size = 40 personas y cada persona tiene un
probabilidad prob = 0.1 de estar infectada, entonces la distribución
del número de personas infectadas dentro del área es:
hist(rbinom(n = 100000, size = 40, prob = 0.1))
# hist(rbinom(n = 100000, size = 40, prob = 0.1),xlim = c(0,40))También podemos expresarlo en términos de proporción de personas
infectadas dividiendo por su tamaño size
hist(rbinom(n = 100000, size = 40, prob = 0.1)/40)
# hist(rbinom(n = 100000, size = 40, prob = 0.1)/40,xlim = c(0,1))En promedio, ¿Qué porcentaje del área tendría un 10% o menos de personas infectadas (es decir, 4 de 40)?
pbinom(q = 4, size = 40, prob=0.1)Ejemplo 2
Podemos usar la distribución beta para describir la proporción de personas vacunadas en una población durante un proceso de vacunación
hist(rbeta(n = 100000, shape1 = 1, shape2 = 3.8))En promedio, ¿Qué porcentaje de la población tendría un 70% o más de personas vacunadas?
1- pbeta(q = 0.7, shape1 = 1, shape2 = 3.8)Referencias
Sparks, A.H., P.D. Esker, M. Bates, W. Dall’ Acqua, Z. Guo, V. Segovia, S.D. Silwal, S. Tolos, and K.A. Garrett, 2008. Ecology and Epidemiology in R: Disease Progress over Time. The Plant Health Instructor. DOI: https://doi.org/10.1094/PHI-A-2008-0129-01. Chapter: Statistical distributions
Más aprendizaje
Para aplicar estos conceptos básicos a un caso particular, se recomienda hacer las prácticas “An outbreak of gastroenteritis in Stegen, Germany” en el sitio web de RECON https://www.reconlearn.org/post/stegen.html
Lecturas recomendadas
Gran parte del contenido de este tutorial básico de R provino de libros conocidos de Hadley Wickham, que en su mayoría están disponibles en línea.
- R for Data Science - versión en español https://es.r4ds.hadley.nz/
- Advanced R http://adv-r.had.co.nz/
- R packages http://r-pkgs.had.co.nz/
También puedes revisar “The Epidemiologist R Handbook” https://epirhandbook.com/ que provee de ejemplos para resolver problemas epidemiológicos y asistir a epidemiólogos en su transisión a R. Si quieres apoyar en la traducción a español, ¡contáctalos!
Sobre este documento
Contribuciones
- Zulma M. Cucunuba: Versión inicial
- Zhian N. Kamvar: Ediciones menores
- Kelly A. Charniga: Ediciones menores
- José M. Velasco-España: Traducción de Inglés a Español
- Andree Valle-Campos: Ediciones menores
Contribuciones son bienvenidas vía pull requests.
Asuntos legales
Licencia: CC-BY Copyright: Zulma M. Cucunuba, 2019
